
关于作者:
Pau Rodríguez 是蒙特利尔 Element AI 的研究科学家。他获得了巴塞罗那自治大学的计算机科学博士学位。他的研究兴趣包括元学习和计算机视觉。
当需要昂贵的专家标注时,图像标注可能是机器学习应用的瓶颈。一些例子包括医学成像、天文学或植物学。
为了缓解这个问题,小样本分类旨在从少量(几个)样本(样本)中训练分类器。一个典型的场景是一样本学习,每个类别只有一个图像。另一个是零样本学习,其中类别以不同的格式提供给模型。例如,我可以告诉你“玫瑰是红色的,天空是蓝色的”,你应该能够在没有实际看到任何图片的情况下对它们进行分类。
最近的研究利用未标记数据来提升小样本性能。一些例子包括标签传播和嵌入传播。这些方法属于“转导式”和“半监督”学习 (SSL) 类别。在这篇文章中,我将首先概述小样本学习领域。然后,我将以标签传播和嵌入传播为例解释转导式和 SSL。
小样本分类
在由 Vinyals 等人 提出的典型小样本场景中,模型会呈现由支持集和查询集组成的情景。支持集包含有关我们想要对查询进行分类的类别的信息。例如,模型可以得到一张计算机和平板电脑的图片,然后它应该能够对这两个类别进行分类。事实上,模型通常会得到五个类别(5 路),每个类别一个(单样本)或五个(五样本)图像。在训练过程中,模型会收到这些情景,它必须学会根据支持集正确猜测查询集的标签。在训练、验证和测试期间看到的类别都是不同的。这样,我们就可以确定模型正在学习适应任何数据,而不仅仅是记忆训练集中的信息。虽然大多数算法使用情景,但不同的算法家族在如何使用这些情景训练模型方面有所不同。接下来,我将介绍三个算法家族:度量学习、基于梯度的学习和迁移学习。
度量学习方法
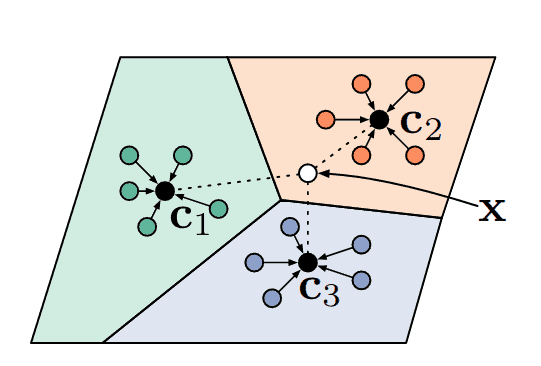
目前,小样本学习最简单也是最流行的方法是度量学习。在这种范式中,模型学习将图像投影到一个空间中,在这个空间中,给定一些距离度量,相似的类别彼此靠近,而不同的类别则相距更远。也许最著名的小样本学习模型是k 近邻,它会将查询分配给与其最近的支持相同的标签。事实上,原型网络 (Snell 等人),目前最流行的小样本算法之一,就是基于相同的度量学习原理,见图 1。
基于梯度的方法
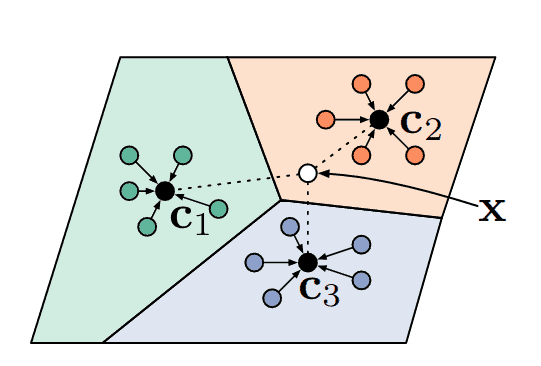
这类算法,例如模型无关元学习或 MAML (Finn 等人),学习一个好的网络初始化,以便通过在给定支持集上微调模型来解决任何问题。在每次训练迭代中,MAML 会同时优化网络参数的多个副本,然后通过所有这些优化进行反向传播来更新原始权重。MAML 启发了许多后来的研究,例如 Reptile、iMAML 或 ANIL。
迁移学习方法
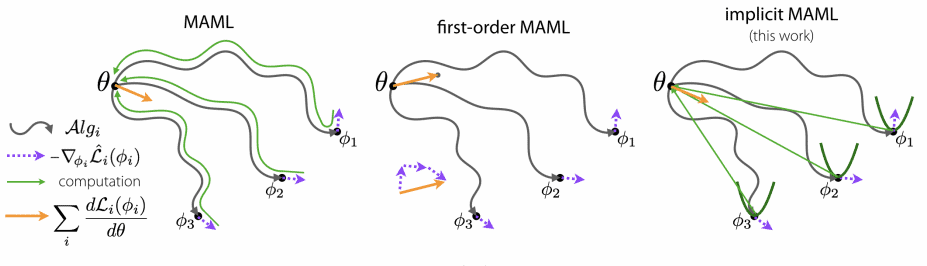
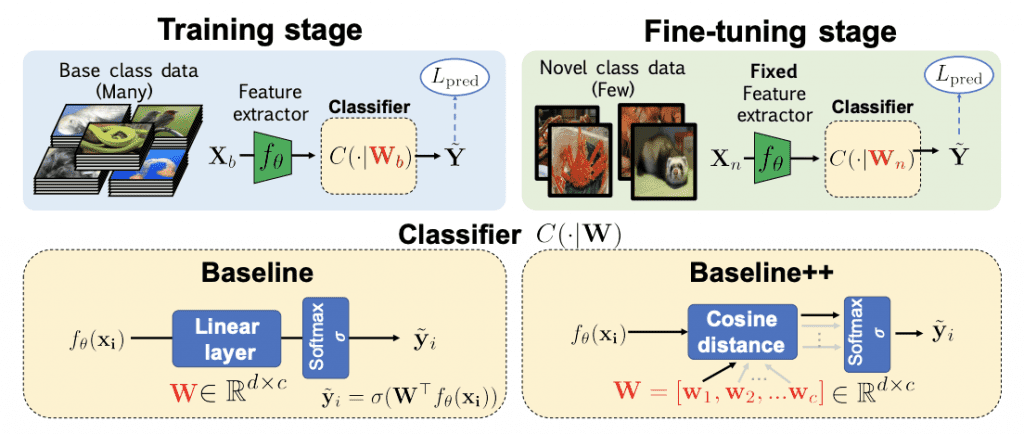
最近,迁移学习方法已成为小样本分类的最新技术。像无遗忘动态小样本视觉学习 (Gidaris & Komodakis) 这样的方法在第一阶段预训练一个特征提取器,然后在第二阶段,它们学习重用这些知识以在新的样本上获得一个分类器。由于其成功和简单性,迁移学习方法在两篇最近的论文 (Chen 等人、Dhillon 等人) 中被称为“基准”。
不用说,还有很多没有在这里引用但值得花时间的工作,以及贝叶斯或生成方法。但是,这篇文章的目的是介绍转导式小样本学习,它是在简要介绍小样本学习之后进行的。
转导式小样本学习
机器学习中最常见的分类场景是归纳式场景(或者说不是这样,正如你将要看到的那样…)。在这种情况下,我们必须学习一个函数,该函数为任何给定输入生成一个标签。与之不同的是,在转导式场景中,模型可以访问我们想要分类的所有未标记数据,它只需要为这些样本生成标签(而不是为所有可能的输入样本生成标签)。在实践中,转导被用作一种半监督学习形式,其中我们有一些未标记的样本,模型可以从这些样本中获得有关数据分布的额外信息以进行更准确的预测。在小样本学习中,转导式算法会利用情景中的所有查询,而不是将它们单独处理。对这种场景的一种可能的批评是,每个类别通常有 15 个查询,而且在现实生活中获取平衡的未标记数据是不现实的。正如 Nichol 等人 在他们的论文中指出的那样,请注意,由于批归一化,许多小样本算法已经是转导式的。
最近,由于 Liu 等人 的工作,转导式算法在小样本分类中越来越受欢迎。他们利用了一种名为标签传播的转导式算法。那么,标签传播是什么呢?
标签传播
标签传播 (Zhu & Ghahramani) 是一种算法,它通过图的节点传递标签信息,其中节点对应于标记和未标记的样本。该图是基于嵌入之间的一些相似性度量构建的,因此图中彼此靠近的节点被认为具有相似的标签。与其他算法(例如 KNN)相比,其主要优势在于标签传播尊重数据的结构。以下是我做的一个例子

虽然这种传播算法是迭代的,但 (Zhou 等人) 提出了一个封闭形式的解决方案。该算法如下所示
1. 计算节点的相似性矩阵 $W$。在这个矩阵 $W_{i,j}$ 中,节点 $i$ 和节点 $j$ 之间的相似性。对角线被设置为零以避免自我传播。
2. 然后计算 $S=D^{-\frac{1}{2}}WD^{-\frac{1}{2}}$ 拉普拉斯矩阵,它可以被看作是图的矩阵表示。
3. 获取传播器矩阵 $P=(I-\alpha S)^{-1}$。基本上,这个矩阵告诉你从一个节点到另一个节点需要传递多少标签信息。
4. 最后,给定一个矩阵 $Y$,其中每一行都是节点的独热编码,大多数行都是由 0 组成(未标记的样本),而一些行在相应的类别中包含一个 1,则最终标签 $\hat{Y}$ 为 $PY$。
矩阵求逆是一个昂贵的操作,这使得它难以应用于大型数据集,但幸运的是,小样本情景很小。因此,Liu 等人 提出了一个用于小样本学习的转导式传播网络 (TPN),如以下图所示
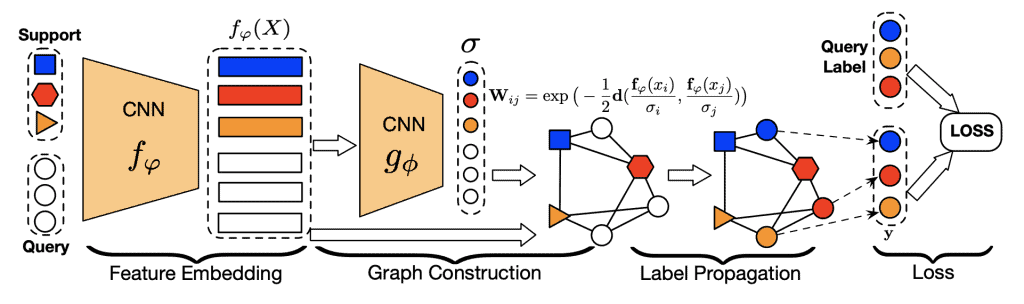
图 5. 转导式传播网络。 图像特征通过 CNN 提取。然后,这些特征用于使用相似性矩阵 $W$ 构建一个图。为了使非相邻节点为 0,使用了径向基函数。由另一个神经网络 ($g_{\Phi}$) 预测。来源:Liu 等人
这个想法是,支持集的标签通过图传播到查询集。这种架构被证明非常有效,获得了最先进的结果,并启发了新的最先进方法,例如嵌入传播。
嵌入传播
正如 Chapelle 等人 解释的那样,半监督学习和转导式学习算法对数据做出了三个重要假设:平滑性、聚类和流形假设。在最近的 嵌入传播 论文(发表于 ECCV2020)中,作者基于第一个假设来改进转导式小样本学习。具体来说,这个假设说,在嵌入空间中彼此靠近的点在标签空间中也必须彼此靠近(相似的点具有相似的标签)。为了实现这种平滑性,作者应用标签传播算法来传播图像特征信息,而不是像你在下图中看到的那样传播标签信息
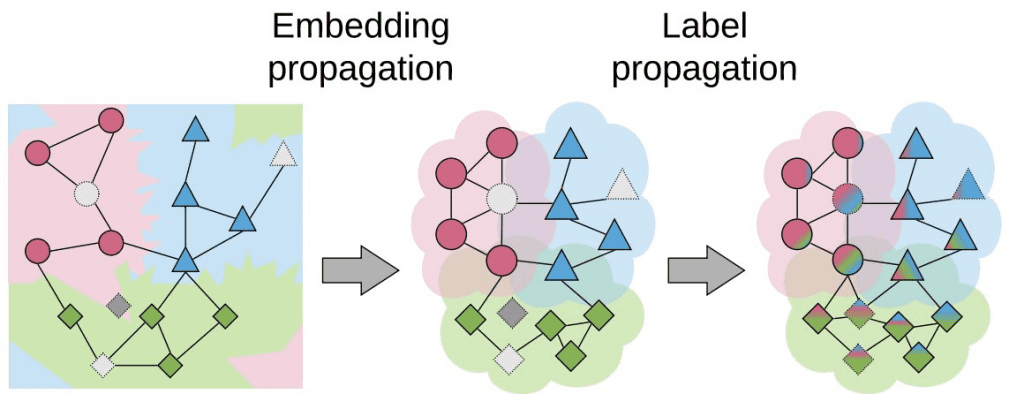
这意味着彼此相似的节点会变得更加靠近,从而提高嵌入空间的密度。因此,应用于这些新的密集嵌入的标签传播会获得更高的性能
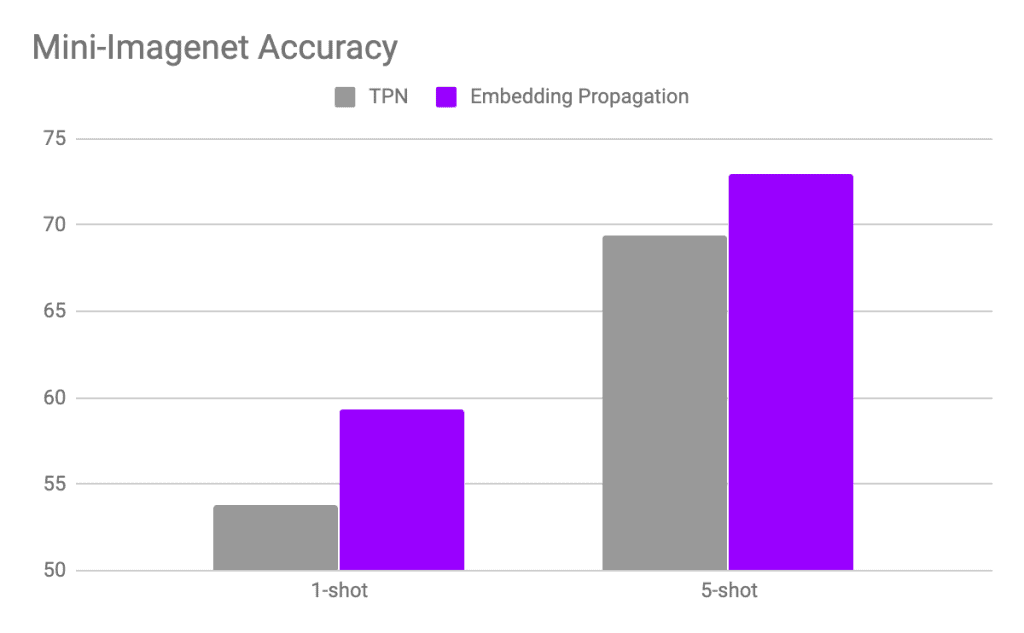
此外,作者表明他们的方法对半监督学习和其他转导算法也有益。例如,他们将嵌入传播应用于Gidaris 等人提出的少样本算法,平均性能提高了 2%。作者在他们的github 存储库中提供了 PyTorch 代码。您只需添加 3 行代码即可在您的模型中使用它。
import torch from embedding_propagation import EmbeddingPropagation ep = EmbeddingPropagation() features = torch.randn(32, 32) embeddings = ep(features)
结论
转导学习已成为少样本分类中的一个反复出现的主题。在这里,我们看到了什么是转导学习以及它如何提高少样本算法的性能。我们还看到了它的一些缺点,例如未标记数据的平衡假设。最后,我解释了最近的嵌入传播算法来改进转导少样本分类,并给出了关于它为何有效的一些直觉。






